01
退回
排序
排序的概念
排序的分类
- 内部排序算法(数据可完全加载入内存,所有操作在内存中进行)
- 就地排序算法(In-place Sorting):这些算法只需要少量的额外内存(如 O(1) 或 O(log n))来进行排序。
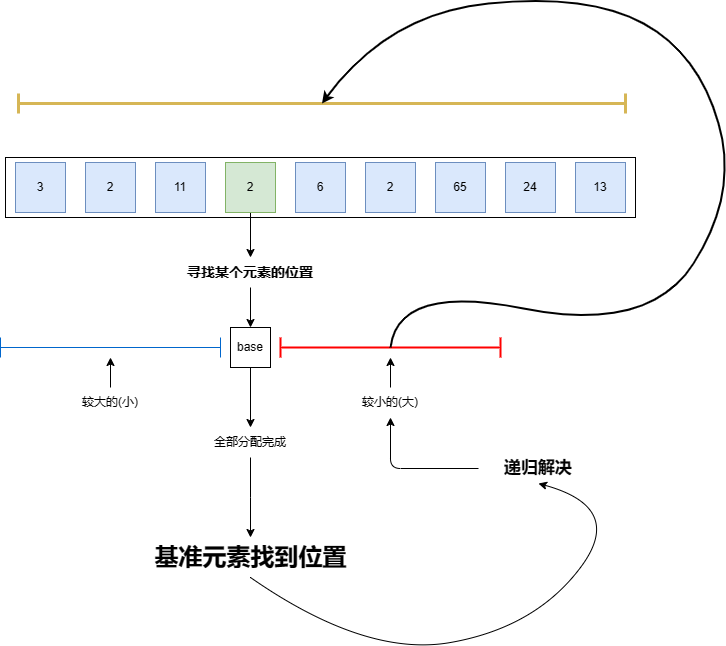
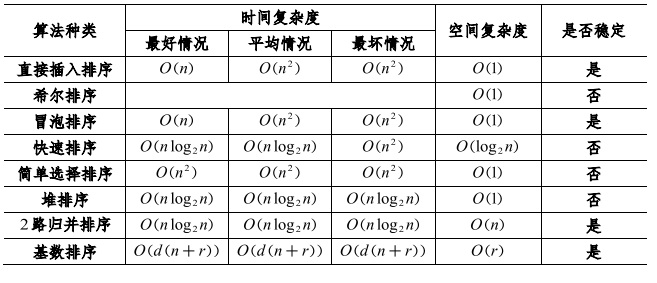
- 快速排序(Quick Sort):时间复杂度$ O(n log n)$,空间复杂度 $O(log n)$。
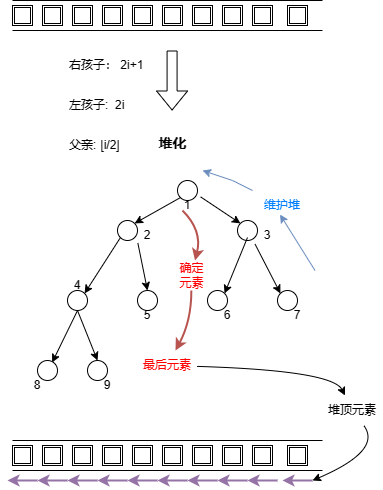
- 堆排序(Heap Sort):时间复杂度$ O(n log n)$,空间复杂度 $O(1)$。
- 插入排序(Insertion Sort):时间复杂度 $O(n^2)$,空间复杂度 $O(1)$。
- 选择排序(Selection Sort):时间复杂度 $O(n^2)$,空间复杂度 $O(1)$。
- 冒泡排序(Bubble Sort):时间复杂度 $O(n^2)$,空间复杂度 $O(1)$。
- 非就地排序算法(Non-in-place Sorting):这些算法需要额外的存储空间来辅助排序,通常是 O(n) 空间。
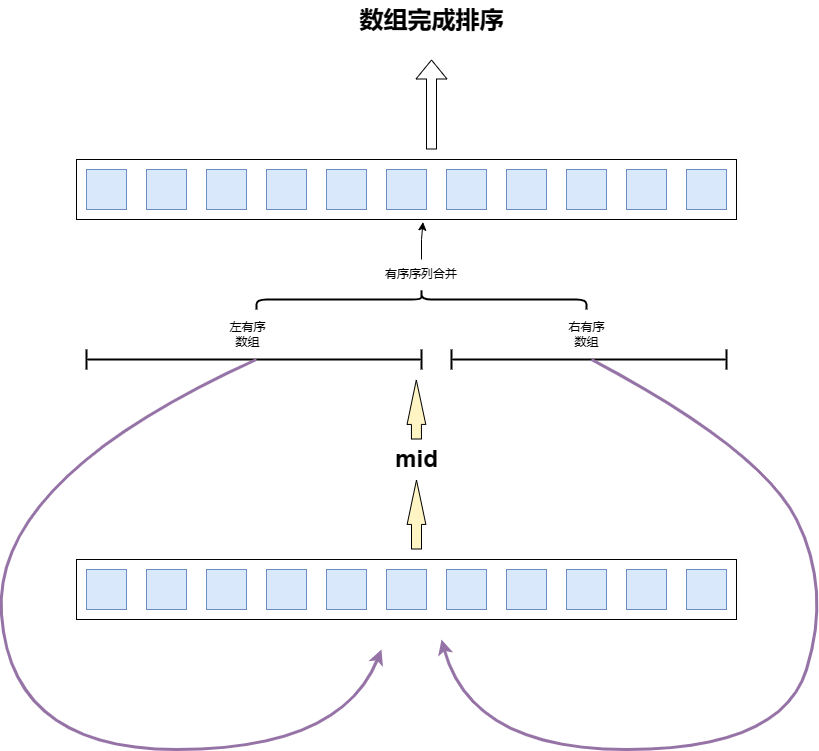
- 归并排序(Merge Sort):时间复杂度$O(n log n)$,空间复杂度 $O(n)$。
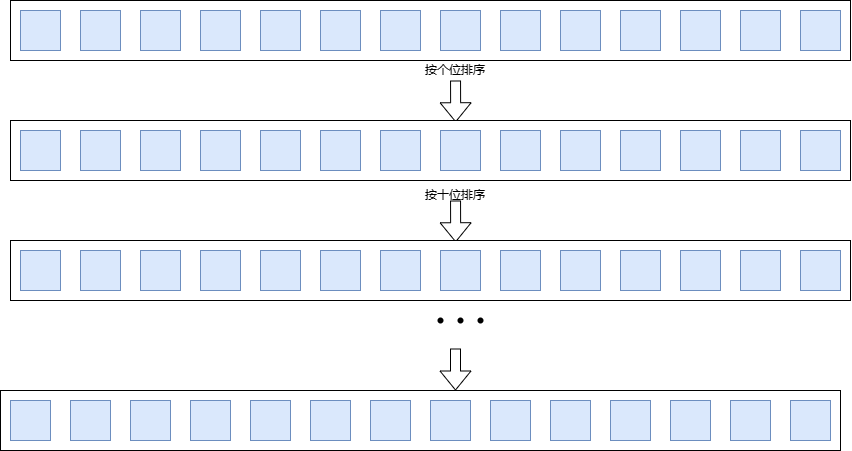
- 基数排序(Radix Sort):时间复杂度$O(nk)$,空间复杂度 $O(n + k)$,其中 k 是数字的位数。
- 计数排序(Counting Sort):时间复杂度 $O(n + k)$,空间复杂度 $O(n + k)$。
外部排序算法(数据集过大,无法全部加载入内存,必须依赖外部存储)
外部排序算法通常用于需要处理非常大规模数据集的场景,例如数据库管理系统中的排序操作。常见的外部排序算法是归并排序(Merge Sort),通常采用归并排序的外部实现来处理大规模数据。
- 外部归并排序(External Merge Sort):这种排序方法将数据划分为多个块,每个块先用内部排序算法排序,然后将排序后的块通过归并算法合并。
- 替代合并排序(Replacement Selection):在进行归并操作时,使用一种特殊的选择方式减少磁盘访问次数。
排序算法
- 冒泡排序
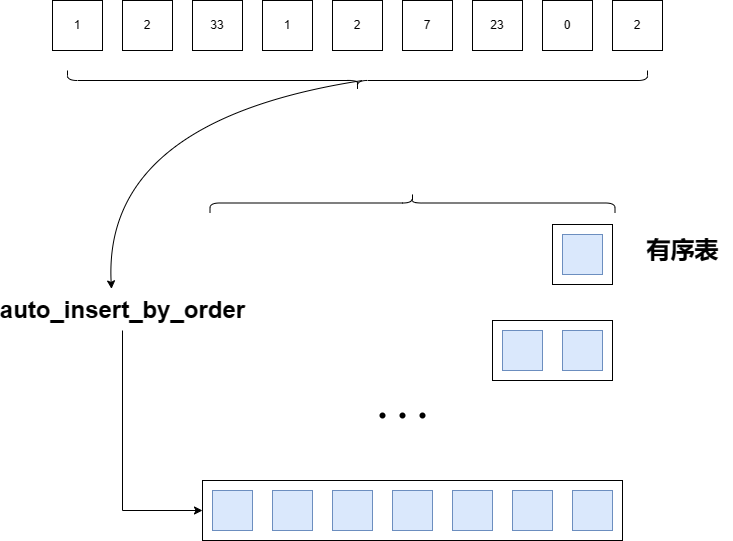
- 插入排序
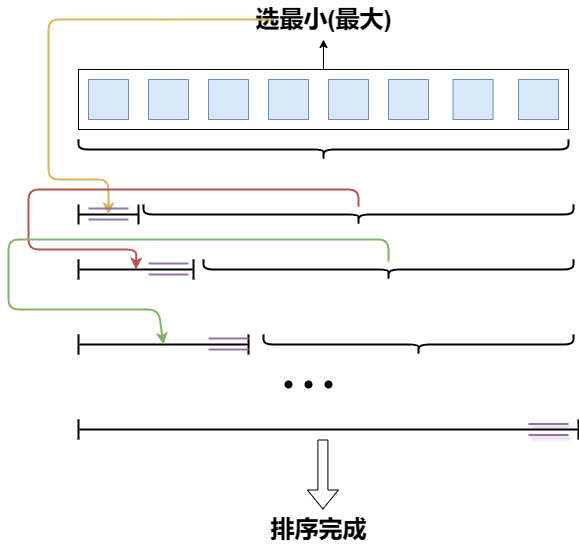
- 选择排序
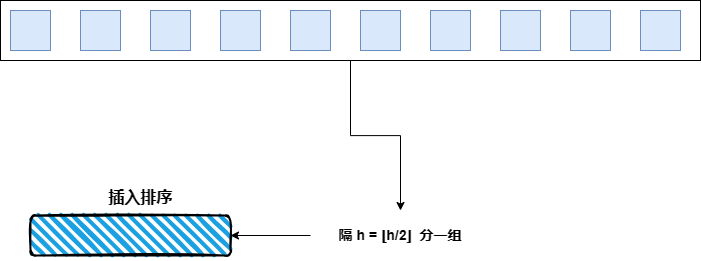
- 希尔排序 无最优的间隔,一般选择:
h = n / 2, n / 4, ..., 1
- 归并排序
- 快速排序
- 堆排序
- 计数排序
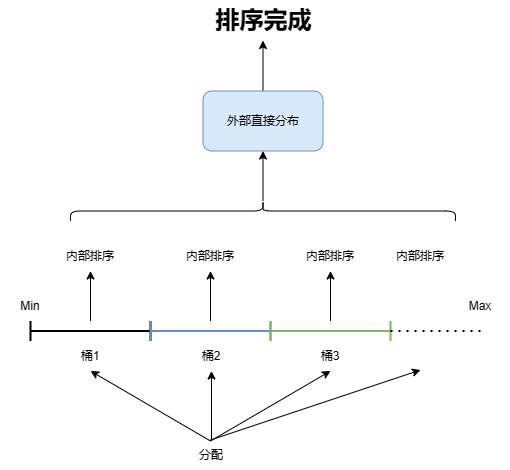
- 桶排序
- 基数排序